Personnel
This research was carried out in a ph.d. study by Erik Jørgensen and supervised by Associate Professor Olav Breinbjerg and Associate Professor Peter Meincke.
Background
Computational electromagnetics (CEM) allow for accurate modeling of physical systems in combination with an accurate numerical solution of either differential or integral formulations of Maxwell's equations. The on-going advances in computer technology has internationally spawned an enormous increase in research on CEM and its application to many practical engineering problems, e.g., antenna design, electromagnetic compatibility, and bio-electromagnetics. This research is directed at developments and implementations of techniques that facilitate very accurate analysis and synthesis of large-scale, complex electromagnetic systems which today remain at, or beyond, the limits of CEM.
CEM techniques based on integral equations are advantageous in systems where electromagnetic waves are radiated in open regions. The equations are usually discretized using the method of moments in which an unknown physical quantity is expanded in terms of a set of known expansion functions. This leads to a linear system of equations with N unknowns, where N is the is the number of expansion functions. The computational requirements are then at least proportional to N2 in terms of both computer time and memory. Since N may be very large these requirements are beyond the capabilities of today's computers (e.g., 76 GByte RAM if N=100.000). There are two possible ways to overcome this bottleneck: Reduce the computational requirements to something lower than N2, or simply reduce N (without sacrificing the accuracy). Recently, the so-called fast methods such as the multilevel fast multipole method have obtained computational requirements proportional to N*log(N) which allows for problems with millions of unknowns. The research conducted at AFG follows the second path, aiming at reducing N significantly without sacrifizing the accuracy.
AFG Research
The AFG research in this area is focused on the following three topics:
- Higher order polynomial expansion functions. The functions under investigation are hierarchical vector basis functions that automatically satisfy Kirchoff's continuity law and allow for flexible modeling of the physical system. The number of unknowns can approximately be reduced by a factor of 4 (implying a reduction by a factor of 16 in computer memory) compared to conventional low order expansion functions.
- Hybridization with other techniques. The number of unknowns can be reduced dramatically by combining the method of moments with other techniques that provide a priori knowledge of the physical mechanisms involved. These other techniques are the physical optics method, the physical theory of diffraction, and related techniques.
- Parallelization of the computation. Combining the resources of many separate computers increases the calculation speed and extends the maximum number of unknowns. This distributed memory configuration is low-cost and highly flexible and has been preferred instead of an expensive shared memory configuration where many processors are combined into a single computing unit.
The research goal is to investigate these three topics, develop each of them further, and implement the techniques in an efficient computer code to prove their versatility. This code is being implemented in High Performance Fortran and the Message Passing Interface (MPI) is used for communication in a distributed memory configuration, thus ensuring portability to a variety of computer platforms.
One particular technique has already been developed and tested. This fringe integral equation technique is more efficient than conventional techniques when an impressed source is located in close vicinity of the physical structure. In such cases, a highly peaked current will be induced on the structure which requires a large number of basis functions to obtain an accurate result. The fringe integral equation is not affected by this, since the current peak is treated with analytical techniques and the method of moments is used to solve for the well-behaved fringe current only. The picture below shows the difference between the peaked total current and the well-behaved fringe current (red areas indicate currents with high amplitude). The fringe integral equation technique was recently used to model the radiation pattern of the Danish Rømer satellite and its crossed-slot antenna.
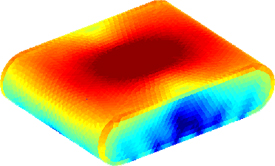
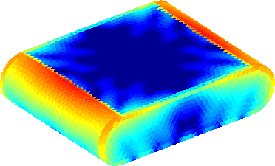
Fig. 1: Induced total (or fringe) current on a 3m*3m*1m box with rounded corners illuminated by a magnetic Hertzian dipole at 300 MHz. The dipole is locate just above the center of the top surface to simulate the radiation from a slot antenna.
Publications
Papers on the fringe integral equation method:
- Erik Jørgensen, Alberto Toccafondi, and Stefano Maci, Fringe integral equation method for a Truncated grounded dielectric slab, IEEE Transactions on Antennas and Propagation, vol. 49, no. 8, August 2001.
- Erik Jørgensen, Peter Meincke, and Olav Breinbjerg, An efficient fringe integral equation method for optimizing the antenna location on complex bodies, IEEE Antennas and Propagation Society Symposium, Boston, July 2001.
- Erik Jørgensen, Peter Meincke, and Olav Breinbjerg, A fringe dual-surface magnetic field integral equation for three-dimensional structures with nearby sources, Proceedings of the 17th Annual Review of Progress in Applied Computational Electromagnetics, ACES 2001, p. 231-237, Monterey, California, March 2001.
- Erik Jørgensen, Alberto Toccafondi, and Stefano Maci, Integral equation solution for truncated slab structures by using a fringe current formulation, Proceedings of the IEEE Antennas and Propagation Society Symposium, p. 2546-2549, Orlando, Florida, July 1999.
Copies of the papers can be obtained by contacting Peter Meincke.
[Back to Research projects]