Personnel
PostDoc Enrica Martini
Professor Olav Breinbjerg
Period
November 2005 - August 2007
Funding
Technical University of Denmark, in the framework of the Hans Christian Oersted Postdoc Programme
Background
The determination of an antenna’s radiation pattern from near-field measurements via a near-field to far-field (NF2FF) transformation algorithm is a widely adopted technique. In this framework, planar near-field scanning is often preferred for the simplicity of mechanical equipment and transformation algorithms. However, due to the limited size of the scanning area, the resulting pattern is reliable only within an angular region depending on the geometry of the antenna under test (AUT) and on the extension and position of the scan area. Thus, a large scanning area is required to enlarge the angular region in which the resulting pattern is reliable. Since long measurement times and complex facilities are required to cover large scan areas, a technique allowing to accurately reconstruct the antenna far field starting from a limited number of measured data could significantly speed up and simplify the process of measurement acquisition.
On the other hand, by performing a spherical scanning it is in principle possible to obtain the radiation pattern over the entire angular span of any arbitrary antenna. In this framework, spherical NF2FF transformation techniques based on a modal expansion in spherical waves has been widely used, and the Technical University of Denmark has been active in this field since the early Seventies. However, in many practical cases it can be unpractical or even impossible to perform the measurements on the whole sphere: this is the case for in-situ spherical near-field antenna measurements, and for spherical scanning of large fragile satellite antennas, whose support does not permit the probe to be moved on a full sphere. Hence, a procedure to reduce truncation errors is required.
Description
We propose a technique based on the method of alternating projections to reduce truncation error in planar near field measurements. The method of alternating projections is an iterative algorithm that uses the measured data and prior knowledge to recover a signal, and it has been successfully applied to computer-aided tomography and image restoration problems. A special case of this recursive method is the Gerchberg-Papuolis algorithm, which iteratively computes the transform of a band-limited function, the iterations simply involving the computation of fast Fourier transforms. It has been proved that the mean square error monotonically decreases for an increasing number of iterations and that the procedure is very effective also against noisy data. This algorithm can be directly applied to the extrapolation of the near-field data, since on the measurement plane the spectrum is limited to the visible region. However, the convergence has shown to be generally quite slow.
A more effective iterative procedure, which exhibits a quite fast convergence, is obtained by exploiting the a priori knowledge on the AUT geometry and position. The algorithm is based on the use of the reliable part of the spectrum and on the requirement that the tangential electric field is concentrated on the antenna aperture. Accordingly, the Gerchberg algorithm is applied to continue the spectrum outside the “reliable region” by exploiting the condition of spatial-limitedness of its Inverse Fourier Transform. First, the spectrum is calculated from the truncated measurements and back propagated to the AUT plane. Then, its reliable part is Inverse Fourier transformed to yield an estimate of the field distribution on the AUT plane; this is subsequently modified by setting all the samples outside the antenna aperture to zero. Thus modified, the field distribution is Fourier transformed and the generated spectrum is corrected so that the previous values are restored where the original spectrum is reliable. This process is then iterated until convergence is reached.
The proposed technique has been applied to theoretical as well as measured near field data and in both cases it has turned out to be very effective.
The possibility of extending this approach to the case of spherical measurements is to be investigated.
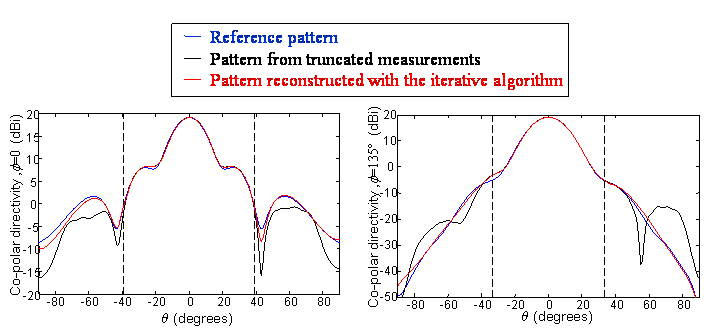
Results of the application of the iterative algorithm to the reconstruction of the pattern of a rectangular horn from truncated planar measurements. The boundaries of the reliable region are shown with vertical dotted lines.
[Back to Research projects]